A sorozat előző része a Python nyelv általános leírását tartalmazta
A python egy dinamikusan típusos nyelv, tehát a következő programrészlet teljesen korrekt:
var=1 print(var) var=1.1 print(var) var="Hallo World" print(var)
Jól láthatóan típusa nem a változónak, hanem az adatnak van típusa, hiszen ugyan abban a változóban egymás után egymástól eltérő típusú értéket tárolhatunk.
A Python 3-ban a következő típusokat lehet használni:
Logikai (Boolean)
A logikai típusnak értelem szerűen két értéke lehet:
True (igaz)
False(hamis)
A boolean típussal a logikai műveleteket lehet elvégezni, illetve feltételes utasításokban használni az értékeiket. (Egy későbbi cikkben részletezem)
Szám (Numeric) típusok:
Egész (integer):
a=2
a=-10
Az integer méretének a rendelkezésre álló memória szab határt.
Az egész számokon értelmezett műveletek:
Összeadás
a=2
b=3
c=a+b
Ugyan így a kivonás
a=2 b=3 c=a-b
szorzás
a=2
b=3
c=a*b
Egész osztás (maradékos osztás)
a=2
b=3
c=a//b
maradék meghatározás (modulo)
a=2
b=3
c=a%b
Hatványozás
a=2
b=3
c=a**b
Ahol a a hatványozás alapja b a kitevő.
Lebegőpontos tört (float)
A float típusban tört és egész számokat tárolhatunk.
a=12.3
A leírások szerint a float mérete függ az adott platformtól. Én PC-n és Raspberry PI2-n néztem meg ugyan azt az eredményt kaptam
import sys
print(sys.float_info)
az eredmény:
sys.float_info(max=1.7976931348623157e+308, max_exp=1024, max_10_exp=308, min=2.2250738585072014e-308, min_exp=-1021, min_10_exp=-307, dig=15, mant_dig=53, epsilon=2.220446049250313e-16, radix=2, rounds=1)
Tehát 10-307 tól 10308 nagyságrendben 15 számjegy pontosságra számíthatunk, mind a pozitív, mind a negatív számok esetén
Ez azt jelenti, hogy a legnagyobb ábrázolható szám 308 számjegyű. Én nem emlékszem, hogy ekkora számot bármikor is használtam volna, ennek ellenére van értelme. Ha osztani szorozni kell kevesebb figyelmet kell fordítani a műveletek sorrendjére, hogy ne csússzunk ki a számábrázolási korlátokból.
A lebegőpontos számokkal már értelmezhető az osztás
a=2
b=3
c=a/b
Komplex számok
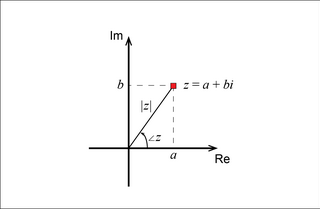
A komplex számokat a+bi formában szoktuk felírni. Kiválóan használhatóak például elektromos áramkörök leírására.
Az i immaginárius tagot definíció szerint négzetgyök(-1)-ként definiáljuk, tehát a komplex számokon értelmezhető a negatív számok négyzetgyöke.
A komplex számokon az összes fent említett művelet elvégezhető, kiegészítve a negatív számokból való négyzetgyökvonással.
import math
var=sqrt(-12)
String
A string változókban szövegeket tárolhatunk. A változó hosszát a rendelkezésre álló memória korlátozza.
a='Hallo' b='World' c=a+' '+b
Az értékadásnál azt, hogy stringről beszélünk ‘ vagy ” jellel jelölhetjük. A két jelölés egyenértékű, azonban a lenti példákkal megmutatom, hogy miért praktikus a kétféle jelölés:
a="Jhon's car" b='Petőfi Sándornak tulajdonított mondás: "Hol a szabadság, ott van a haza." '
A stringek különleges tulajdonsága, hogy nem megváltoztathatóak. A stringek kezeléséről külön cikkben írunk.